Getting started - a single particle¶
In this tutorial, we’ll simulate the stochastic dynamics of a single
nanoparticle. We model clusters of nanoparticles using the
magpy.Model class. In this case we only have a single particle in
our cluster. The first step is to import magpy.
In [1]:
import magpy as mp
To create our model, we need to specify the geometry and material properties of the system. The units and purpose of each property is defined below.
| Name | Description | Units |
|---|---|---|
| Radius | The radius of the spherical particle | m |
| Anisotropy | Magnitude of the anisotropy | J/m\(^3\) |
| Anisotropy axis | Unit vector indicating the direction of the anisotropy | |
| Magnetisation | Saturation magnetisation of every particle in the cluster | A/m |
| Magnetisation direction | Unit vector indicating the initial direction of the magnetisation | |
| Location | Location of the particle within the cluster | m |
| Damping | The damping constant of every particle in the cluster | |
| Temperature | The ambient temperature of the cluster (fixed) | K |
Note: radius, anisotropy, anisotropy_axis, magnetisation_direction, and location vary for each particle and must be specified as a list.
In [2]:
single_particle = mp.Model(
radius = [12e-9],
anisotropy = [4e4],
anisotropy_axis = [[0., 0., 1.]],
magnetisation_direction = [[1., 0., 0.]],
location = [[0., 0., 0.]],
damping = 0.1,
temperature = 300.,
magnetisation = 400e3
)
Simulate¶
A simulation in magpy consists of simulating the magnetisation vector of the particle in time. In the model above we specified the initial magnetisation vector along the \(x\)-axis and the anisotropy along the \(z\)-axis. Since it is energetically favourable for the magnetisation to align with its anisotropy axis, we should expect the magnetisation to move toward the \(z\)-axis. With some random fluctuations.
The simulate function is called with the following parameters: -
end_time the length of the simulation in seconds - time_step the
time step of the integrator in seconds - max_samples in order to
save memory, the output is down/upsampled as required. So if you
simulate a billion steps, you can only save the state at 1000 regularly
spaced intervals. - seed for reproducible simulations you should
always choose the seed.
In [3]:
results = single_particle.simulate(
end_time = 5e-9,
time_step = 1e-14,
max_samples=1000,
seed = 1001
)
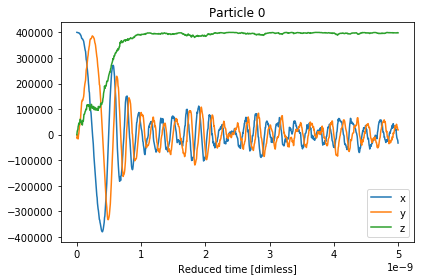
The x,y,z components of the magnetisation can be
visualised with the .plot() function.
In [4]:
results.plot()
Out[4]:
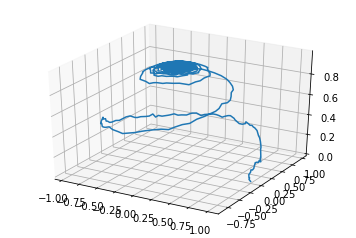
We can also access this data directly and plot it however we like! In this example, we normalise the magnetisation and plot it in 3d space.
In [5]:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
Ms = 400e3
time = results.time
mx = results.x[0] / Ms # particle 0
my = results.y[0] / Ms # particle 0
mz = results.z[0] / Ms # particle 0
fg = plt.figure()
ax = fg.add_subplot(111, projection='3d')
ax.plot3D(mx, my, mz)
Out[5]:
[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7f4f95319a58>]